Competitive Programming with AlphaCode

I'm excited to share more on our latest project, AlphaCode - a system to write programs, able to reach roughly median human performance in coding competitions. And that's median competitive programmer performance, not median programmer or median human! In addition to our paper and [cached]official blog post, you can also find my personal take below.

Problem Setup

Coding competitions are difficult even for experienced programmers. Before writing the first character of a program, the first step is to understand the natural language problem description: often spanning several paragraphs in length, problem descriptions do not directly describe the required algorithm, but rather present the problem in declarative form, only describing what is desired, now how to achieve it:

[cached]Backspace

You are given two strings $s$ and $t$, both consisting of lowercase English letters. You are going to type the string $s$ character by character, from the first character to the last one.

When typing a character, instead of pressing the button corresponding to it, you can press the "Backspace" button. It deletes the last character you have typed among those that aren't deleted yet (or does nothing if there are no characters in the current string). For example, if $s$ is "abcbd" and you press Backspace instead of typing the first and the fourth characters, you will get the string "bd" (the first press of Backspace deletes no character, and the second press deletes the character 'c'). Another example, if $s$ is "abcaa" and you press Backspace instead of the last two letters, then the resulting text is "a".

Your task is to determine whether you can obtain the string $t$, if you type the string $s$ and press "Backspace" instead of typing several (maybe zero) characters of $s$.

Input
The first line contains a single integer $q$ $(1 \leq q \leq 10^5)$ - the number of test cases.

The first line of each test case contains the string $s$ $(1 \leq |s| \leq 10^5)$. Each character of $s$ is a lowercase English letter.

The second line of each test case contains the string $t$ $(1 \leq |t| \leq 10^5)$. Each character of $t$ is a lowercase English letter.

It is guaranteed that the total number of characters in the strings over all test cases does not exceed $2 \cdot 10^5$.

Output
For each test case, print "YES" if you can obtain the string $t$ by typing the string $s$ and replacing some characters with presses of "Backspace" button, or "NO" if you cannot.

You may print each letter in any case (YES, yes, Yes will all be recognized as positive answer, NO, no and nO will all be recognized as negative answer).

An example description for a problem of medium difficulty.

After understanding the problem, the model is then faced with the task of not only coming up with the right algorithm to solve it, but also doing so efficiently - solutions are executed under tight time and memory constraints! In fact, the hardest problems often cannot be solved in Python, but require C++ solutions.

Approach

In AlphaCode, we tackled this problem in multiple steps:

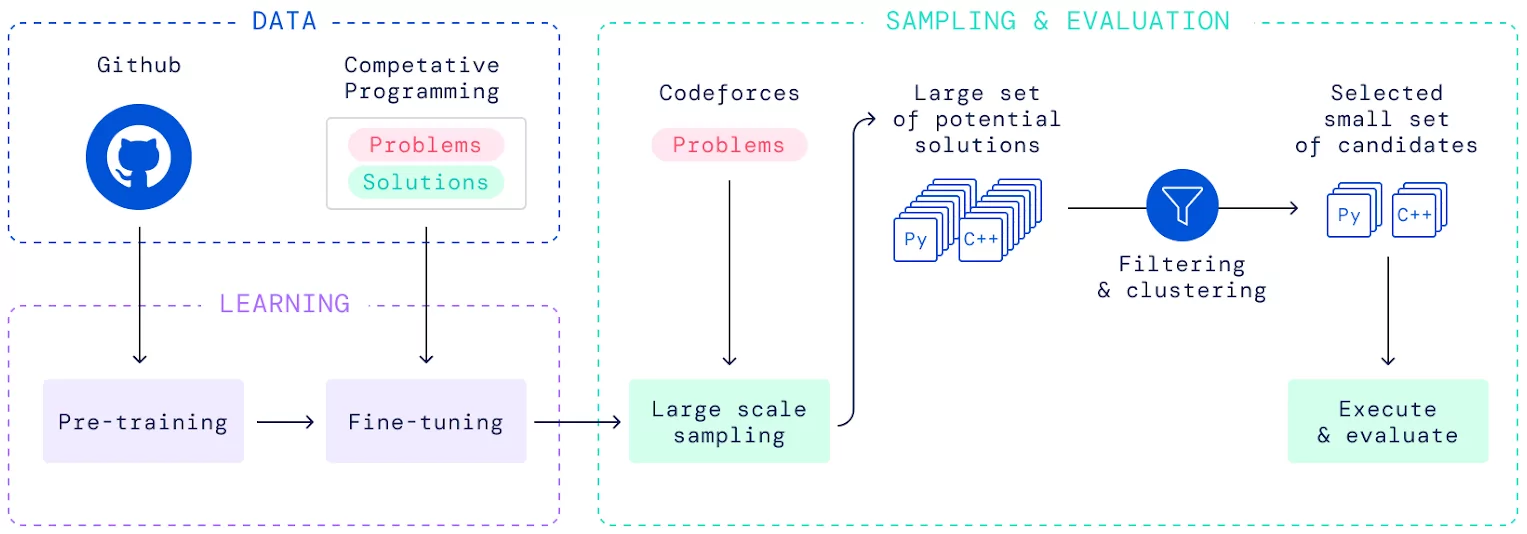
First we collected a large dataset of competitive programming problems and solutions (released as [cached]CodeContests), as well as a collection of open-source code from GitHub.

We used the GitHub dataset to pre-train a large transformer model¹ using standard language modeling losses² to understand code in any of the widely used programming languages³. Next we used our CodeContests datest to finetune the model to generate programs for coding competitions.

With our fully trained model in hand we can now start generating solutions for whichever problem we want to solve. We annotate the problem description with the programming language we want the model to use, then start generating programs: sampling one token at a time, always feeding the selected token back into the model as a basis for the next one.

Solution

This is a solution for the [cached]Backspace problem from above, generated by AlphaCode:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

t=int(input())
for i in range(t):
    s=input()
    t=input()
    a=[]
    b=[]
    for j in s:
        a.append(j)
    for j in t:
        b.append(j)
    a.reverse()
    b.reverse()
    c=[]
    while len(b)!=0 and len(a)!=0:
        if a[0]==b[0]:
            c.append(b.pop(0))
            a.pop(0)
        elif a[0]!=b[0] and len(a)!=1:
            a.pop(0)
            a.pop(0)
        elif a[0]!=b[0] and len(a)==1:
            a.pop(0)
    if len(b)==0:
        print("YES")
    else:
        print("NO")

Solving the problem involved several steps:

• The program needs to run over number of test cases specified in the input (lines 1 - 2).
• The task is to determine whether string t can be produced from string s, so two strings must be read from the input (lines 3 - 4).
• Python strings are immutable, so first we need to create lists of the individual holding the individual characters (lines 5-10).
• Starting at the end, if the last letters match we can proceed to the next letter (lines 11-17).
• If the letters don't match, then we have to remove the last letter. Pressing backspace always deletes two letters: The letter backspace was pressed instead of, and the letter before it (lines 18-22).
• If every letter was matched we can report success (lines 23-26).

Note that the code is not perfect, e.g. the c variable is unnecessary.

Sampling

Of course, we don't need to stop at one generated program - we can generate as many samples as we want⁴, as long as we have some way to select amongst them.

In AlphaCode, we employ two mechanisms for this selection:

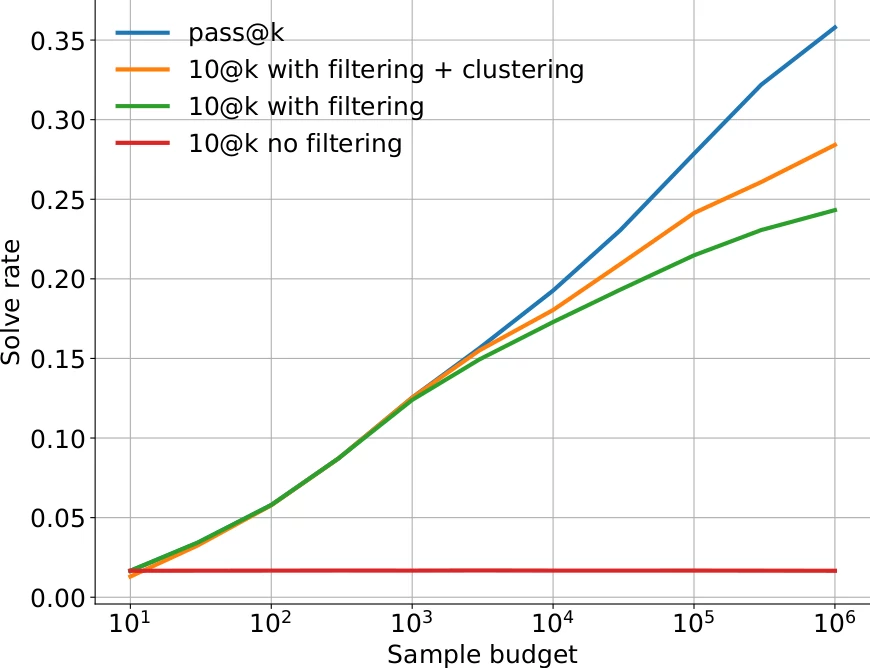
1. We only keep samples that pass the example tests provided in the problem description. These tests are usually pretty short and simple, but enough to weed out programs that are completely incorrect. With our current models, between 80% and 99% of samples are syntactically correct, depending on language⁵ and model size. However, only 0.4% - 0.7% of samples pass all public tests⁶, allowing us to discard more than 99% of samples.
2. For the samples that do pass the public tests we perform a further selection step: we cluster all samples that are syntactically different, but (probably) semantically different. We do this by training a separate model to generate plausible test case inputs based on the problem description, then grouping all samples that produce the same outputs for these generated inputs.

Combined, these two techniques allow us to effectively make use of a very large number of samples:

Dataset

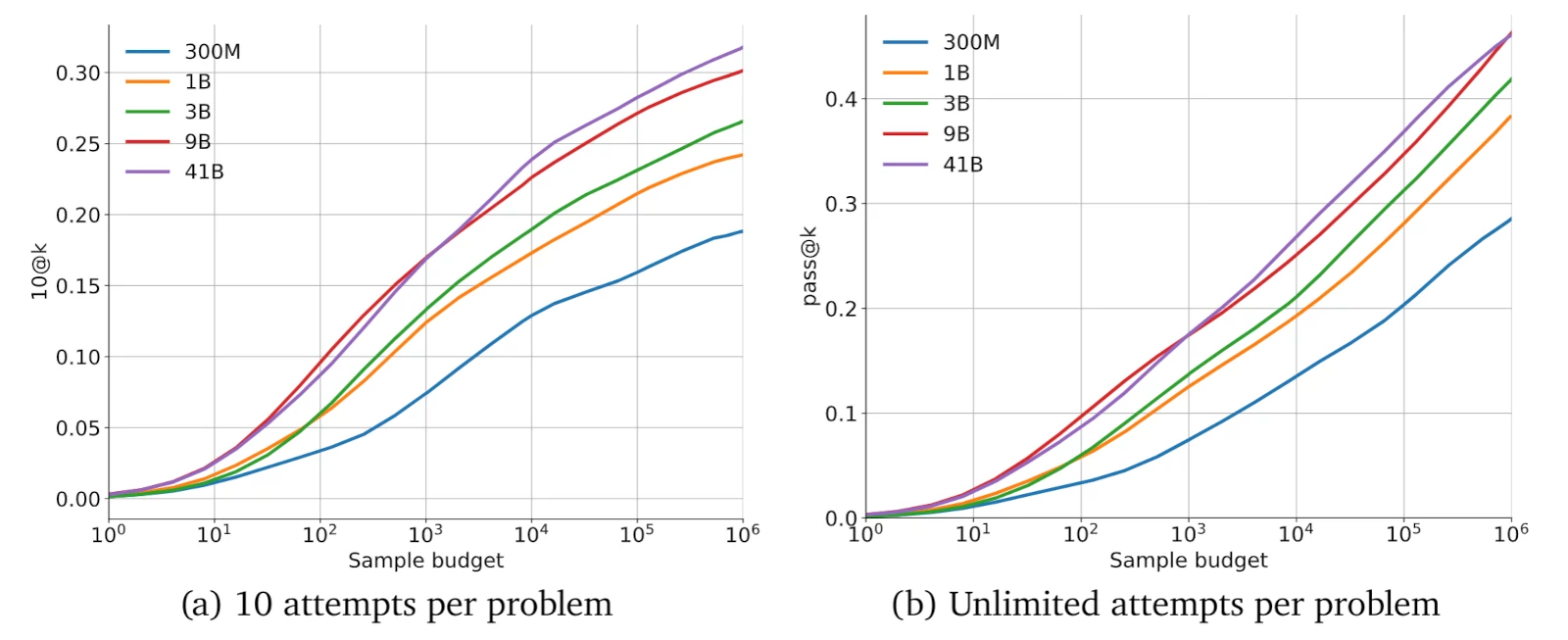
Creating the [cached]CodeContests dataset was a big part of the success of our system. Collecting a large number of solutions, both correct and incorrect, was important to be able to effectively finetune our models without overfitting. The number of distinct problems is especially important, every doubling of the number of problems in our dataset increase the solve rate by a few percentage points.

Just as important however was the focus on accurate evaluations by ensuring we have a large number of test cases for each problem. Existing datasets often suffer from false positives due to insufficient test coverage: if only a handful of tests are present and all of them have the same expected output, then even solutions with wildly incorrect algorithms or hardcoded answers can appear to pass.

To avoid this issue, we generated a large number of extra test cases by mutating existing inputs and collecting the expected output from the correct human solutions. We futher only used problems where we have at least 5 different test cases with at least two different outputs.

Solve rate on the new [cached]CodeContests dataset that we introduce in our paper scales with model size, reaching above 30% for our largest models. Solve rate also scales log-linearly with respect to overal sampling compute - making efficient sampling very important.

Evaluation

To really put AlphaCode to the test we also decided to participate in actual competitions on the [cached]Codeforces platform. This helps ensure that we did not overfit to our dataset, or make mistakes in our evaluations. For evaluation we used the 10 most recent competitions at the time of writing ⁷.

When limited to a maximum of 10 submissions per problem, AlphaCode achieved a ranking of top 54th percentile, roughly average human competitor performance⁸. For most problems far fewer solutions were submitted, on average 2.4 submssions per solved problem. This corresponds to an estimated Codeforces Elo of 1238, within the top 28% of users who participated in at least one contest in the last 6 months.

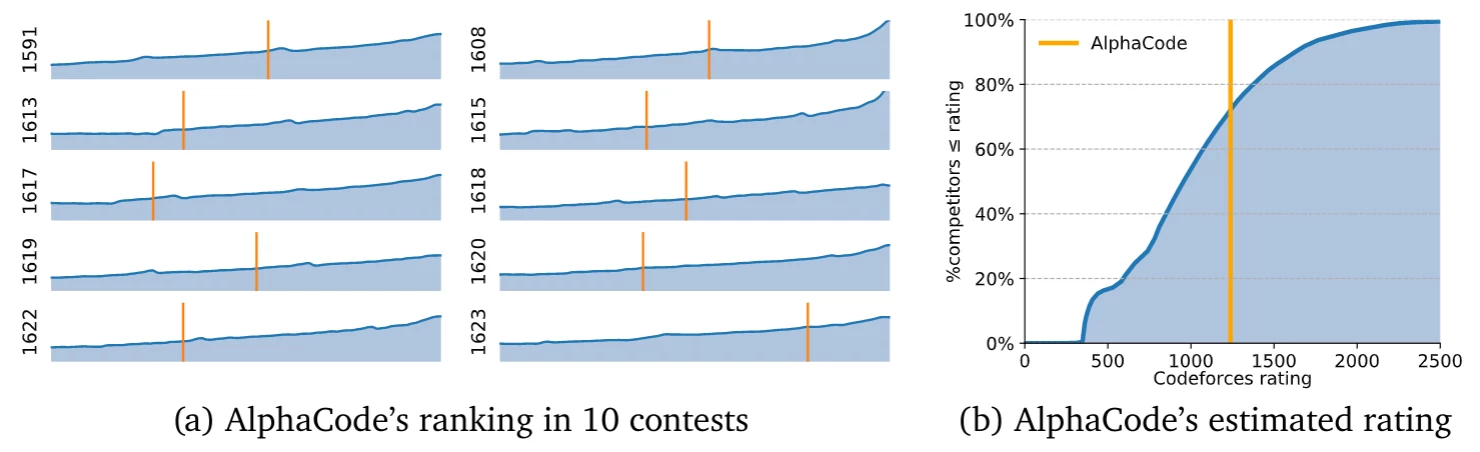
Removing the limit of 10 submissions can increase the solve rate further, reaching 49.7th percentile with an average of 29 submissions per solved problem.

Visualization

Finally, to peak a bit under the hood of AlphaCode and understand a little of what it is doing when it generates programs, we built a [cached]visualization of the attention scores throughout the model⁹. These scores show which parts of the problem description and program generated so far AlphaCode was paying attention to when generating each token in the program:

• The model has an idea of which methods are available on std::cout, and attends to the example output to determine the argument for the precision setting.
• Attends to the relevant parts of the description to determine how to compute the output.
• Understanding the [cached]backspace key in the example problem from above.
• With commentary from Petr Mitrichev, world-class competitive programmer.

Send me your favourite examples and I'll include them here!

To learn more about what transformers are and how attention works, check out [cached]The Illustrated Transformer.

For a whole lot more interesting details and ablations, please check out our full paper.

I will leave you with [cached]Asimov, programming and the meta ladder.

Tags: ai, ml, transformers, programming