After extending to arbitrary action spaces and offline RL, we recently published our next step in generalizing MuZero: Stochastic MuZero, which learns and plans with a stochastic model of the environment that can model not only a single deterministic outcome of our actions, but rather a full set of possibilities.
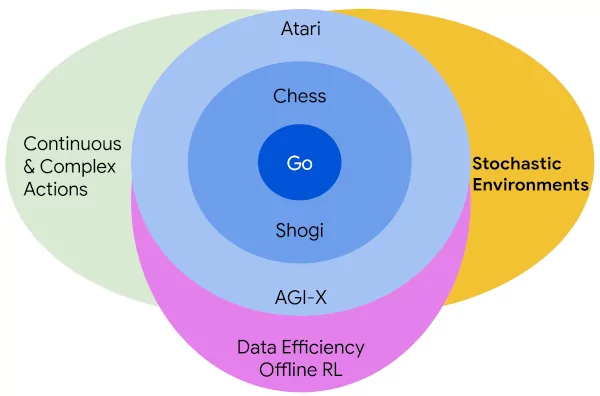
Previous approaches such as AlphaZero and MuZero have achieved very good results in fully-observed deterministic environments, but this type of environment is insufficiently general to model many problems and real world tasks. Beyond the stochasticity inherent in many domains (think roll of the dice or draw of the cards), partially observed environments (hidden cards, fog of war) may also appear stochastic to the agent. Stochastic MuZero presents a more general approach that can handle all of these domains.
The fundamental principle of Stochastic MuZero is the factorization of state transitions into two parts:
- a deterministic, action a_t conditioned transition from state s_t to afterstate as_t
- a stochastic transition from afterstate as_t to the next state s_{t+1}, where each transition is associated with a chance outcome c_t^i.
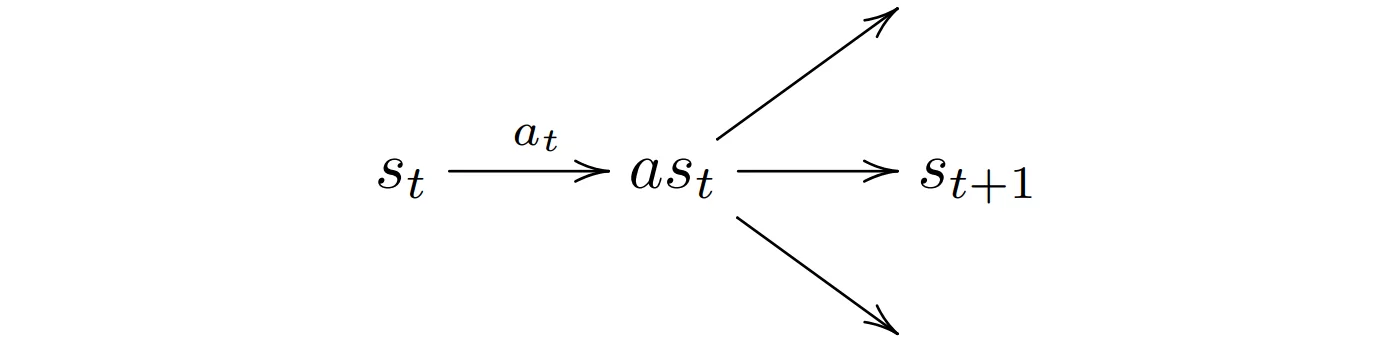
An afterstate as is the hypothetical state of the environment after an action is applied but before the environment has transitioned to a true state. For example in backgammon, the afterstate corresponds to the board state after one player has played its action but before the other player had the chance to roll the dice. This use of afterstates allows us to separate the effect of an action from the stochastic effects in the environment.
Planning
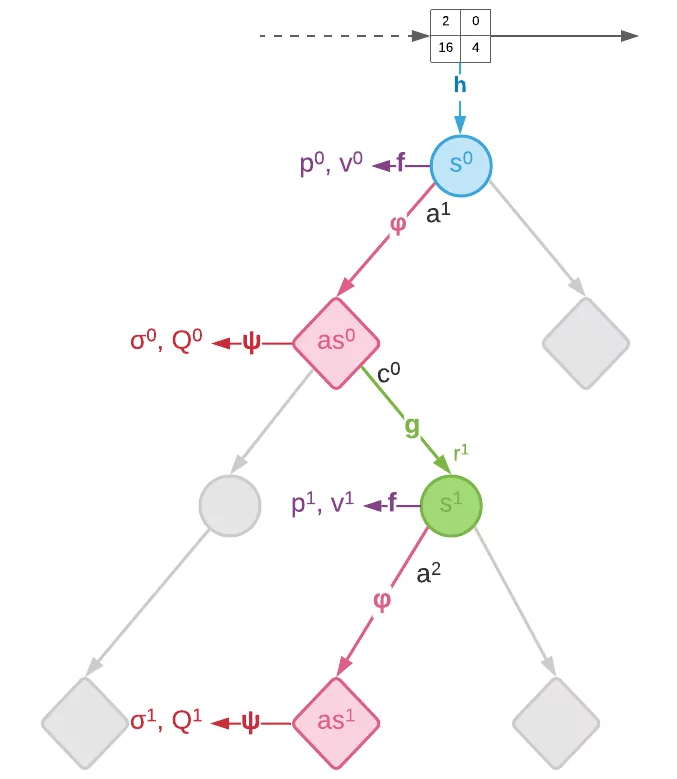
The use of afterstates means that the search tree for MCTS now contains two different types of nodes:
- decision nodes (blue circle), corresponding to states s, with outgoing edges for all possible actions a from this state.
- chance nodes (red rhombus), corresponding to afterstates as, with outgoing edges for the possible chance outcomes c.
The two node types alternate along the depth of the tree, with a decision node always at the root of the tree. At decision nodes actions are selected according to pUCT as in MuZero, whereas at chance nodes edges are always sampled according to the chance probability c \sim Pr(c | as).
Training
To learn afterstates, Stochastic MuZero extends the standard MuZero model with two additional functions: afterstate dynamics \varphi and afterstate prediction \psi.
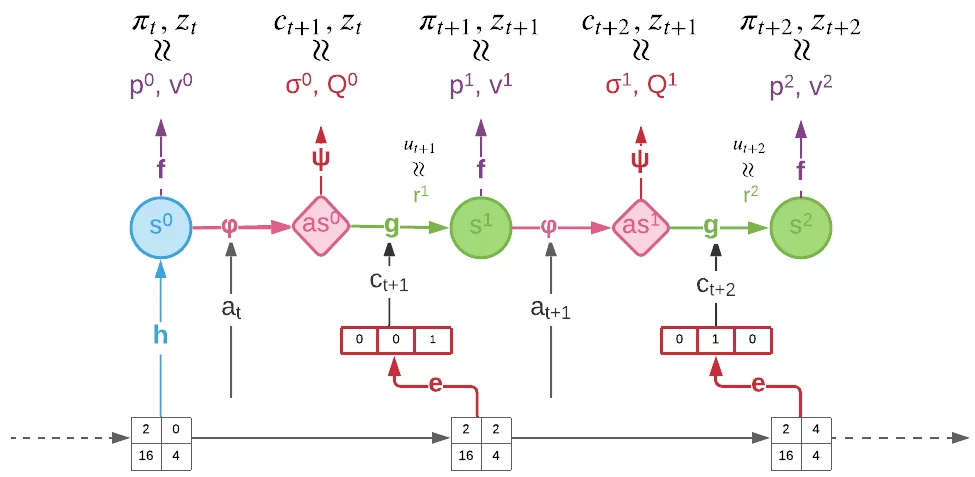
To train this extended model end-to-end, Stochastic MuZero combines the standard MuZero loss with a chance loss:
L_{w}^{chance} = \sum_{k=0}^{K - 1}l^{Q}({z_{t+k}, Q_{t}^{k}}) + \sum_{k=0}^{K-1}l^{\sigma}({c_{t + k + 1}, \sigma_{t}^{k}}) + \beta \underbrace{\sum_{k=0}^{K - 1} \left\lVert c_{t + k + 1} - c^e_{t+k+1}\right\rVert^2}_\text{VQ-VAE commitment cost}
During training the chance outcomes c are generated using an encoder network from future observations. The modelling of chance outcomes is implemented using a novel variant of the VQ-VAE method with a fixed codebook of one-hot vectors.
Results
To validate the effectiveness of Stochastic MuZero we performed a variety of experiments, cover single- and two-player environments and deterministic and stochastic games.
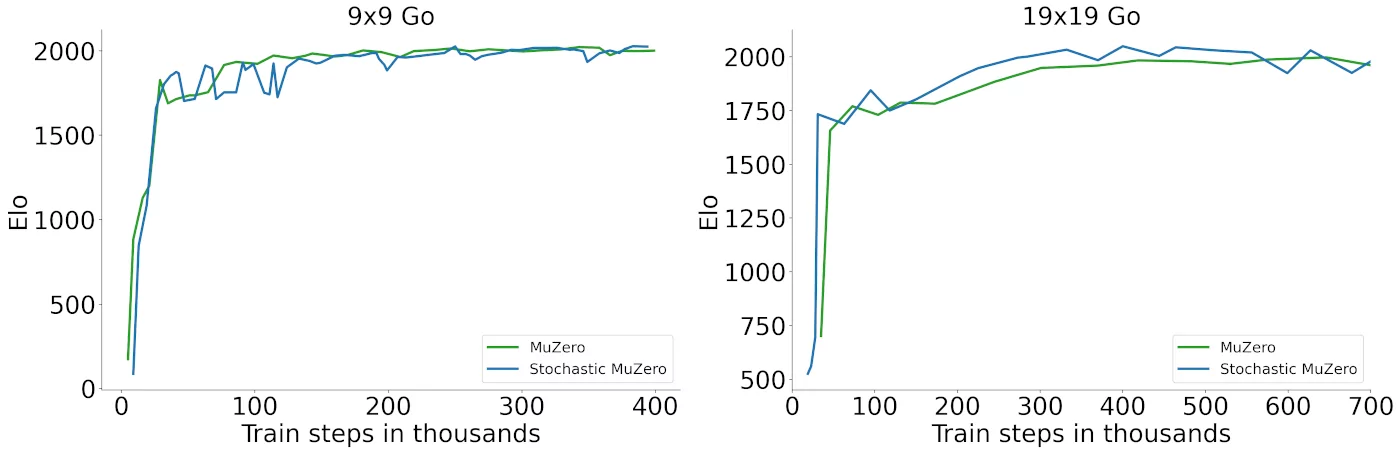
Go
As a first step we verified that it is able to fully recover the performance of standard MuZero in a challenging deterministic environment such as Go:
2048
Next we tested it in on 2048, a popular single-player stochastic puzzle game. While there has been a lot of previous work on this game, the best performing agents to date have relied on explicitly provided knowledge of the simulator. In contrast Stochastic MuZero uses a learned model and no such prior knowledge about the environment, yet is able to achieve superior performance:
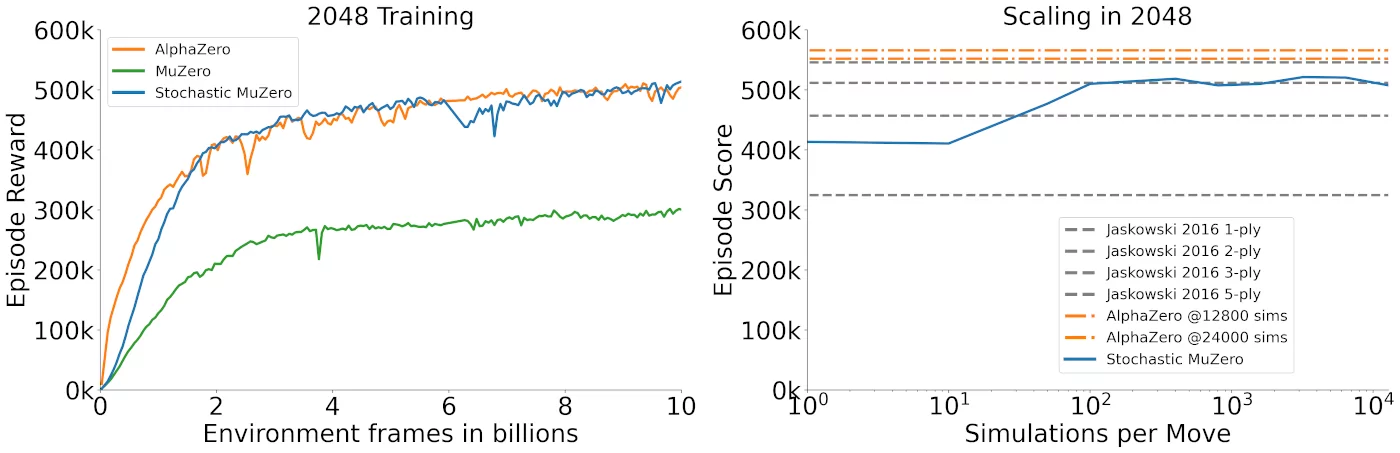
As expected Stochastic MuZero also strongly outperforms MuZero, which lacks the ability to model the stochasticity of the environment.
Backgammon
Finally we also trained Stochastic MuZero on Backgammon, a classic two-player zero-sum stochastic game used as a standard testbed for reinforcement learning since TD-gammon:
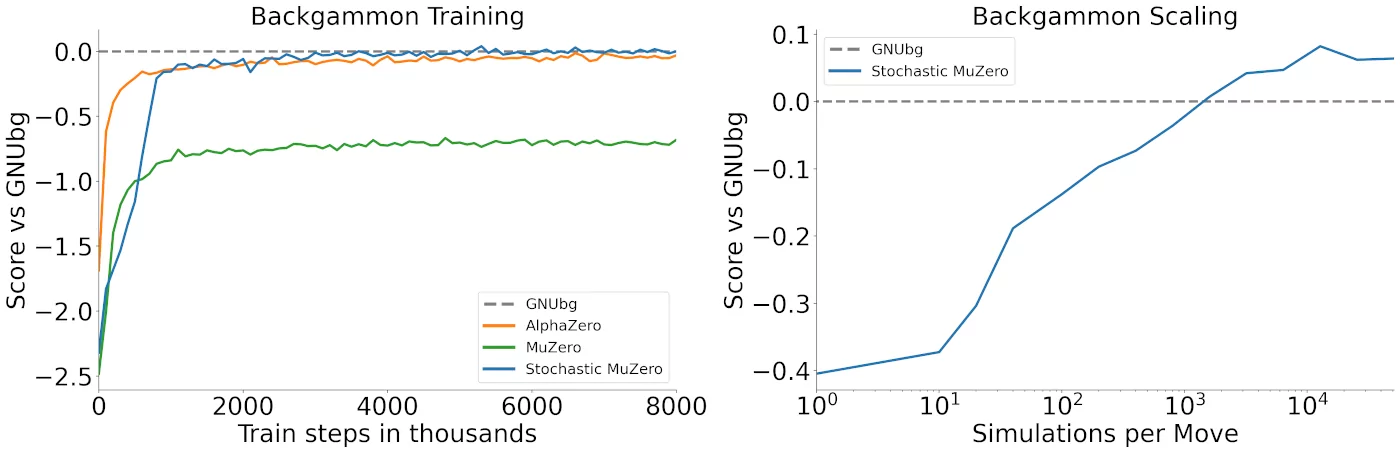
Not only does Stochastic MuZero achieve very good performance, it's playing strength also scales well with the number of simulations during planning, outperforming GNUbg Grandmaster while using a much smaller search budget: GNUbg Grandmaster uses a 3-ply look-ahead search over a branching factor of 20 legal moves on average and 21 chance transitions, for an average of several million positions searched.
Chance Outcomes
In addition to examining the overall performance, we can also directly inspect the distribution of chance outcomes learned by Stochastic MuZero.
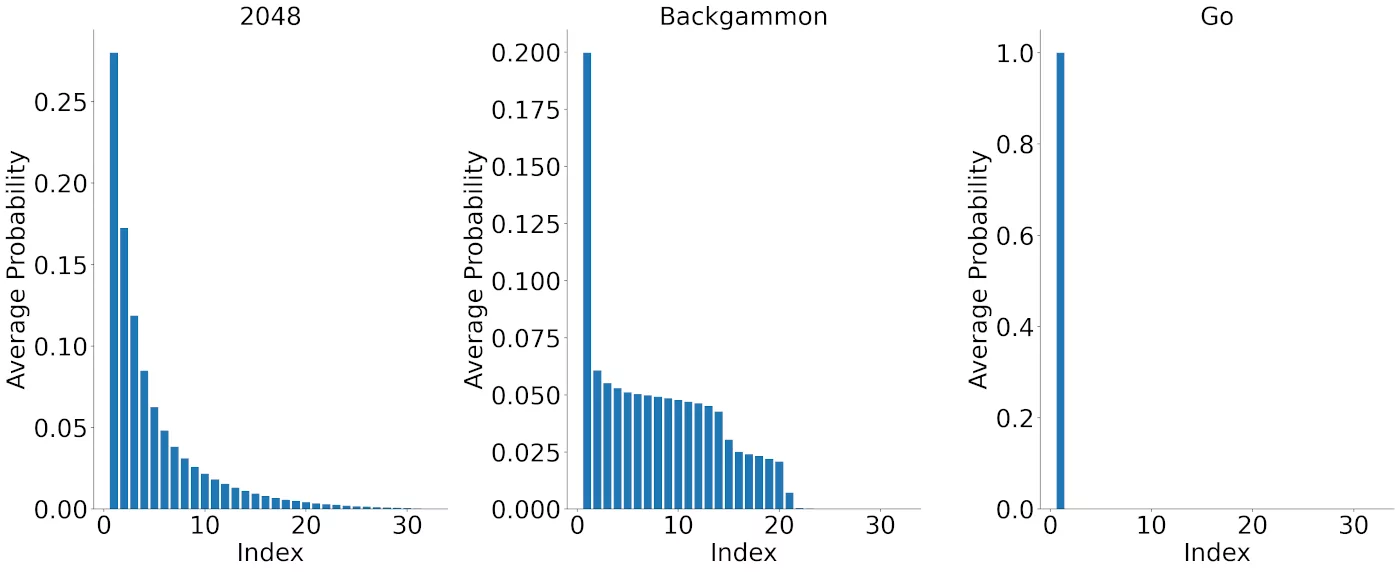
We can observe that in Go, the learned model correctly recovers the deterministic nature of the environment and collapses to a single outcome. In contrast, in the stochastic games the model learns a whole distribution of possible outcomes. In Backgammon, the distribution has a support of 21 outcomes, corresponding to the number of distinct rolls of two dice.
For more details and experiments, please see our full paper and poster.