As of version 3.13, Python is finally getting support for real multi-threading that is not hobbled by the GIL[1]: experimental support for free threading! This means multiple Python threads can now execute at the same time, without needing to compete for the global interpreter lock. In modern machines with hundreds of cores this can speed up CPU-bound programs by two orders of magnitude[2]! Even in ML workloads that only use Python as a DSL with all heavy computation in numpy, JAX etc it is very easy to accidentally be Python interpreter bound[3] - especially in RL algorithms that require more per-episode logic and are less easily batched.
So needless to say, I'm very excited for this! Thanks to the awesome uv package manager, it's extremely easy to test different Python versions:
$ uv run --python 3.14+freethreaded python
Python 3.14.0a4 experimental free-threading build (main, Jan 14 2025, 23:32:57) [Clang 19.1.6 ] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> import sys
>>> sys._is_gil_enabled()
False
First, let's ask our friend Claude for some benchmarks and a visualization script:
"""
Comprehensive Pure Python Threading Benchmark for no-GIL Python (Python 3.13+)
This script benchmarks multiple CPU-bound tasks using different numbers of threads
to evaluate Python's no-GIL threading scalability. All calculations are done in
pure Python without NumPy or other extension modules.
Tests included:
1. Mandelbrot set calculation
2. Matrix multiplication
3. Prime number sieve
"""
full benchmark code, analysis script.
Running this benchmark, we observe reasonable scaling in mandelbrot and prime number sieve but absolutely terrible scaling in matrix multiplication:
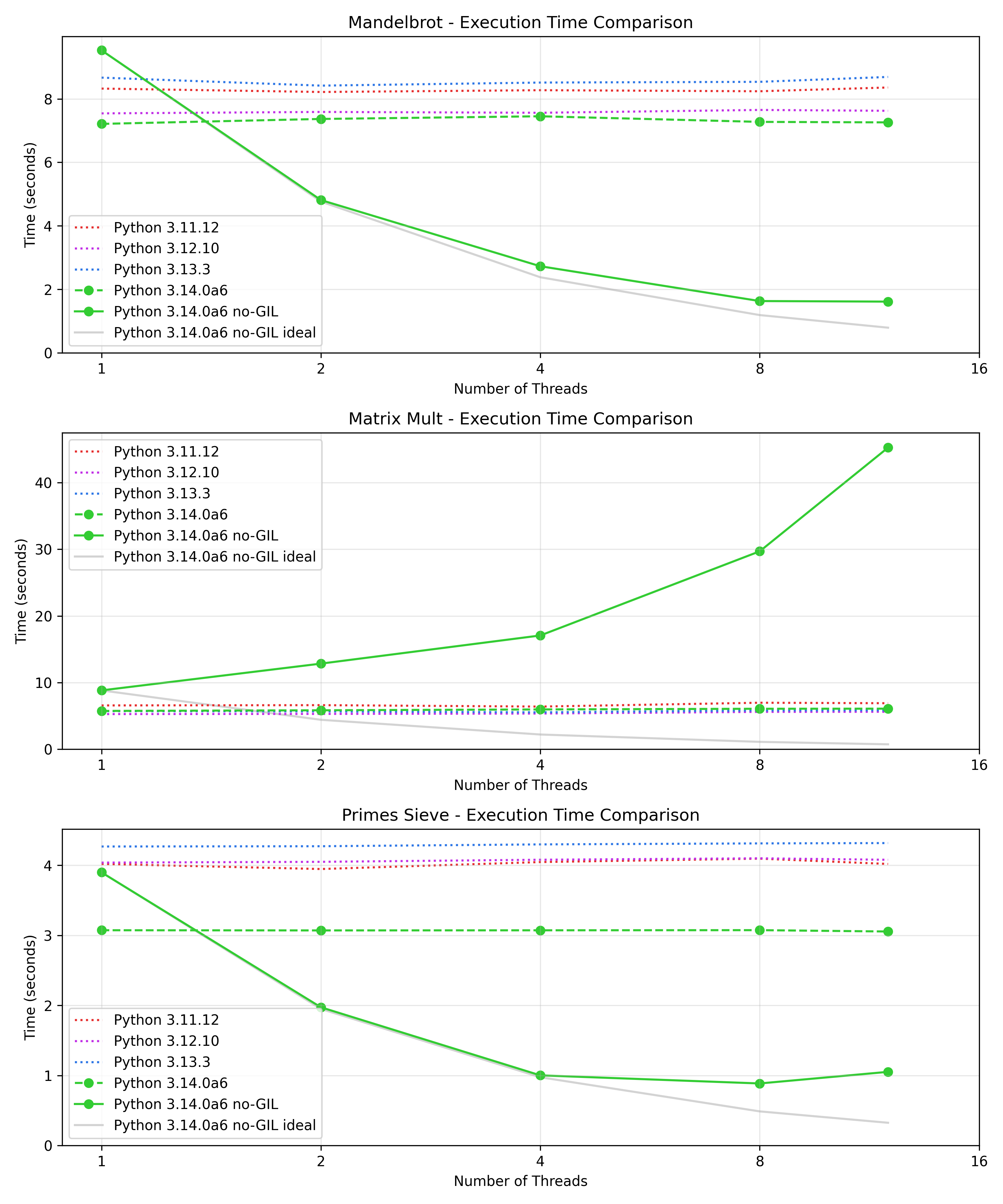
This seems surprising - shouldn't removal of the GIL make threading faster, not slower?
Contention
My first intuition when I see worse performance with increased number of threads is always lock contention. Indeed both the mandelbrot and the prime number sieve benchmark require basically no interaction between the threads, whereas in the matrix multiplication benchmark all threads read from the same matrices and write their results to the same matrix. In principle this should be fine: all access here is read-only, so there should be no need for locking. However, Python doesn't know this - another thread could be concurrently modifying the list, so it needs to acquire a lock for each access.
We can verify that this is the issue by carefully reading the 4000 line C implementation of list copying the list implementation into Claude and asking it to read the C code for us.
According to this, when a non-shared list is accessed from a different thread it acquires a lock to retrieve the requested value:
static PyObject *
list_item_impl(PyListObject *self, Py_ssize_t idx)
{
PyObject *item = NULL;
Py_BEGIN_CRITICAL_SECTION(self);
if (!_PyObject_GC_IS_SHARED(self)) {
_PyObject_GC_SET_SHARED(self);
}
Py_ssize_t size = Py_SIZE(self);
if (!valid_index(idx, size)) {
goto exit;
}
item = _Py_NewRefWithLock(self->ob_item[idx]);
exit:
Py_END_CRITICAL_SECTION();
return item;
}
static inline PyObject*
list_get_item_ref(PyListObject *op, Py_ssize_t i)
{
if (!_Py_IsOwnedByCurrentThread((PyObject *)op) && !_PyObject_GC_IS_SHARED(op)) {
return list_item_impl(op, i);
}
...
}
Supposedly it then also marks the list as shared, so subsequent accesses should be able to take the faster path. It's unclear why this doesn't work in our case, or whether shared lists are just slower in general.
At the very least we can verify that we achieve the expected scaling when passing separate list objects to each thread:
def matrix_multiply_row(args):
"""Multiply one row of matrix A with B (for threading)"""
n, min_i, max_i, A, B = args
results = {}
for i in range(min_i, max_i):
row = [0] * n
for j in range(n):
sum = 0
for k in range(n):
sum += A[i * n + k] * B[k * n + j]
row[j] += sum
results[i] = row
return results
def matrix_multiply(n, A, B, num_threads=1):
"""Multiply two matrices using specified number of threads"""
C = [[0 for _ in range(n)] for _ in range(n)]
# Prepare row tasks
step = 20
tasks = [(n, i, i + step, list(A), list(B)) for i in range(0, n, step)]
# Execute with ThreadPoolExecutor - works for both sequential and parallel
with ThreadPoolExecutor(max_workers=num_threads) as executor:
for rows in executor.map(matrix_multiply_row, tasks):
for i, row in rows.items():
C[i] = row
return C
def generate_matrix(n):
"""Generate a random matrix of size n×n"""
import random
random.seed(42) # For reproducibility
return [random.random() for _ in range(n*n)]
This is obviously unrealistic - we are making n / step copies of both matrices! But it serves to show that the problem is indeed due to sharing the matrix list objects:
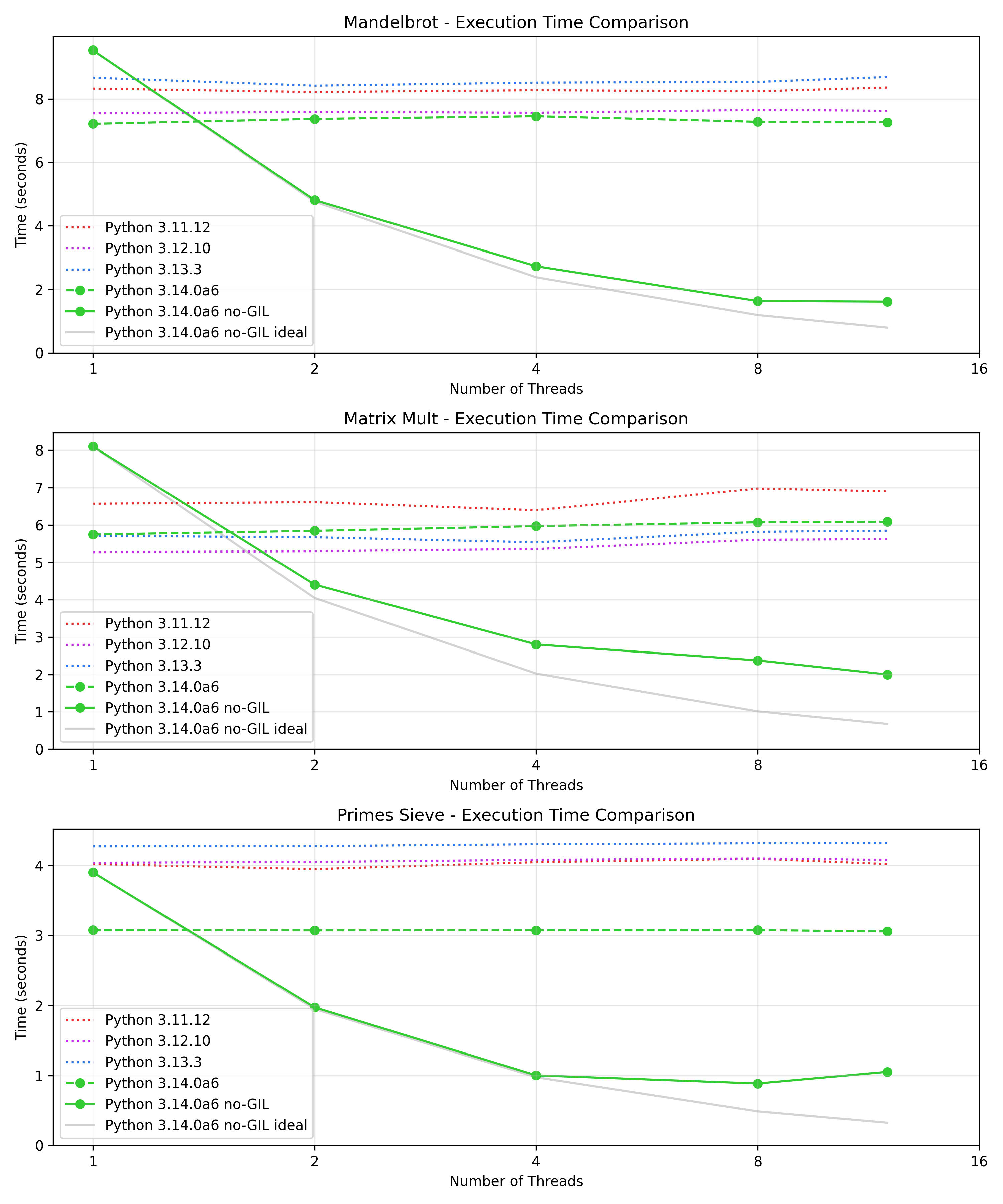
Conclusion
For a more realistic example I wanted to try the matrix multiplication benchmark with a numpy array as well, but unfortunately numpy doesn't yet seem to build with Python 3.14.0a6. I guess it's a preview after all!
Overall no-GIL seems like a clear win if the threads require little or no coordination, and I'm very excited to start adopting it, but great care needs to be taken when operating on a single datastructure from multiple threads. This is not a big limitation: for easy to understand and maintain multi-threaded code you should minimize the interaction between threads anyways.
Update: this issue is fixed in 3.14.0a7 already!!
-
In Python, historically all interpreter data structures were protected by a single lock, the Global Interpreter Lock, GIL for short. This made for a simpler implementation, but also meant that the interpreter could only execute a single Python thread at a time. Native C/C++/Rust extensions could release the GIL to take advantage of more cores, but normal Python code could not. ↩
-
Assuming you didn't rewrite all the performance critical parts in Rust already 😂 ↩
-
see Amdahl's law ↩
Tags: python, programming, threading