We've been working on making MuZero as easy to use as possible, allowing it to be applied to any RL problem of interest. First and foremost, this required us to make some algorithmic extensions.
The original MuZero algorithm achieved good results in discrete action environments with a small action space - classical board games and Atari, with up to a few thousand different actions. However, many interesting problems have action spaces that cannot be easily enumerated, or are not discrete at all - just think of controlling a robot arm with many degrees of freedom, smoothly moving each joint. So far, MuZero could not be applied to these types of problems.
Unsatisfied with this situation, we set out to extend MuZero to the case of arbitrary action spaces - any number of dimensions, any combination of discrete and continuous. The result is [cached]Sampled MuZero, an extension of the MuZero algorithm to be purely sample based, now published at ICML.
As the name implies, in Sampled MuZero both the search and the training of the policy are based on a sample of actions:
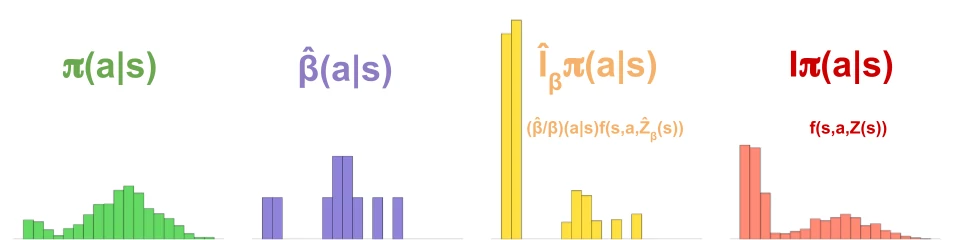
- Instead of enumerating the distribution over all actions $\pi(a | s)$, in each state the Monte Carlo Tree Search (MCTS) only considers a set of candidate actions sampled from the policy: $\hat{\beta} (a | s)$.
- The MCTS produces an improved distribution $\hat{I}_{\beta} \pi(a | s)$ over these candidate actions. To avoid double counting of probabilities, the UCB formula does not use the raw prior $\pi$, but instead the sample-based equivalent $\frac{\hat{\beta}}{\beta} \pi$ - intuitively, a count of how many times each action has been sampled; in the simplest case this is uniform.
- In turn, instead of updating on the probability for all possible actions, the policy is updated on this sampled improvement, leading to a new policy $I \pi(a|s)$.
For the exact derivation of this algorithm, please see the [cached]paper.
This sampled based search works well in all the domains we tested it - from recovering the performance of MuZero on traditional discrete domains such as Go and Atari, to being able to learn high-dimensional continuous control tasks such as the humanoid tasks from state as well as pixel based input:
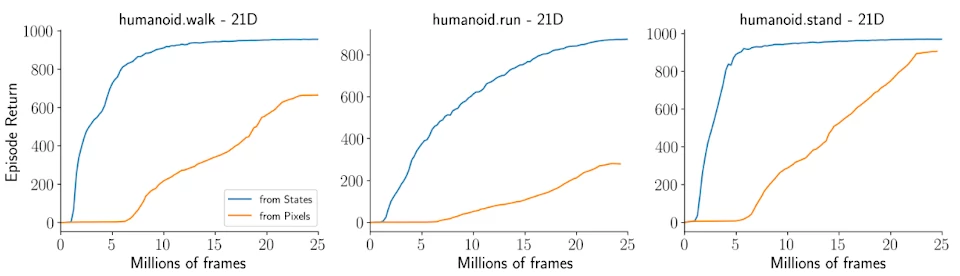
We look forward to seeing which new problems and domains this algorithm will be applied to!
For more details, in addition to the [cached]paper, please also see our poster, and - if you are registered for ICML - also our spotlight talk.