Matrix multiplication is at the foundation of modern machine learning - whether transformers or convolutional networks, diffusion models or GANs, they all boil down to matrix multiplications, executed efficiently on GPUs and TPUs. So far the best known algorithms have been discovered manually by humans, often optimized for specific use cases.
The most famous is probably the [cached]Strassen algorithm to multiply two 2x2 matrices using only 7 instead of the naive 8 multiplications:
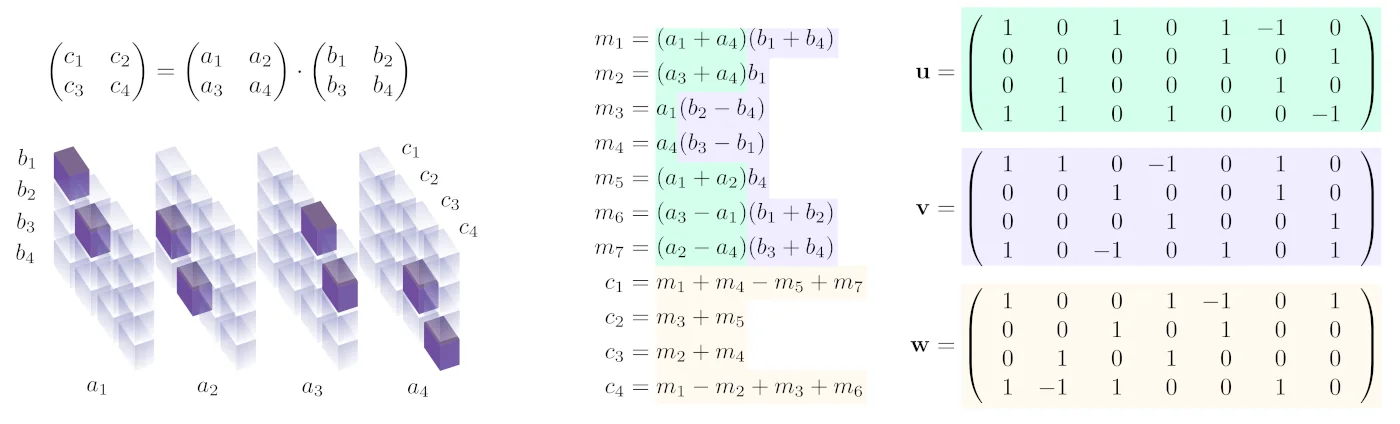
Through clever addition and subtraction of the individual elements of the a and b matrices this algorithm is able to combine the intermediate results into the elements of c with only 7 multiplications in total, at the cost of more additions and subtractions. This algorithm can also be applied recursively to much larger matrices, splitting them into smaller pieces.
This trade-off between multiplications and additions often results in a speed-up in practice, especially for large matrices, as additions are cheaper than multiplications - as you've surely noticed when performing arithmetic by hand.
AlphaTensor
Discovering algorithms such as Strassen is very difficult - the best known algorithm for 2x2 and 4x4 matrices has not been improved in more than 50 years!
To tackle this challenge we are introducing [cached]AlphaTensor, an RL agent that discovers novel, efficient and provably correct algorithms for the multiplication of arbitrary matrices. AlphaTensor works by treating matrix multiplication as a tensor decomposition game, where the matrix multiplication algorithm corresponds to the low-rank decomposition of a 3D tensor (the m equations in the figure above). The goal of the game is to minimize the number of steps it takes to decompose the tensor; at each step in the game the agent selects which locations of the a and b matrices to combine, and to which c locations the result should be added:
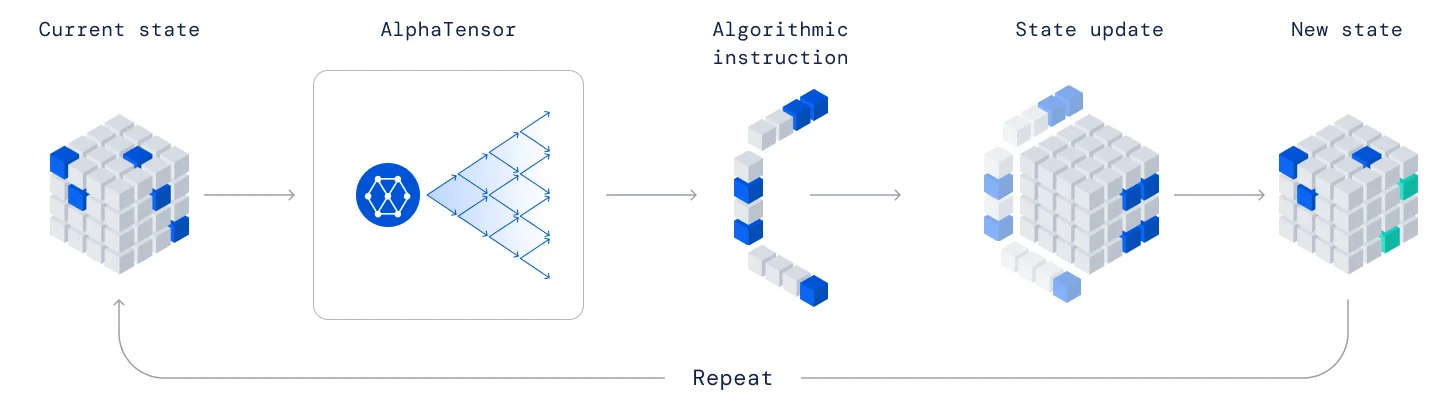
AlphaTensor is based on [cached]AlphaZero, well known for achieving superhuman performance in board games such as Go and chess. AlphaTensor also uses the Sampled AlphaZero extension to deal with the extremely large action space (more than $10^{12}$ actions in most interesting cases).
To properly tackle the tensor based nature of the TensorGame, AlphaTensor introduces a further set of inovations:
- A transformer-based neural network architecture which treats all three cyclical transpositions of the 3D tensor equally: each layer applies attention to all three pairs of tensor axis in turn, generalizing sequential attention to the tensor case.
- The policy auto-regressively samples actions using a transformer decoder, cross-attending to the final embedding produced by the torso transformer.
- Synthetic demonstrations are used to bootstrap learning: While decomposing a tensor is NP-hard, the inverse task of constructing a tensor from factors is trivial. We generate random factors, combine them into a tensor, then train the network to recover the factors.
- We use change of basis as data augmentation, both when constructing the initial tensor to decompose and when preparing the input for the network.
Results
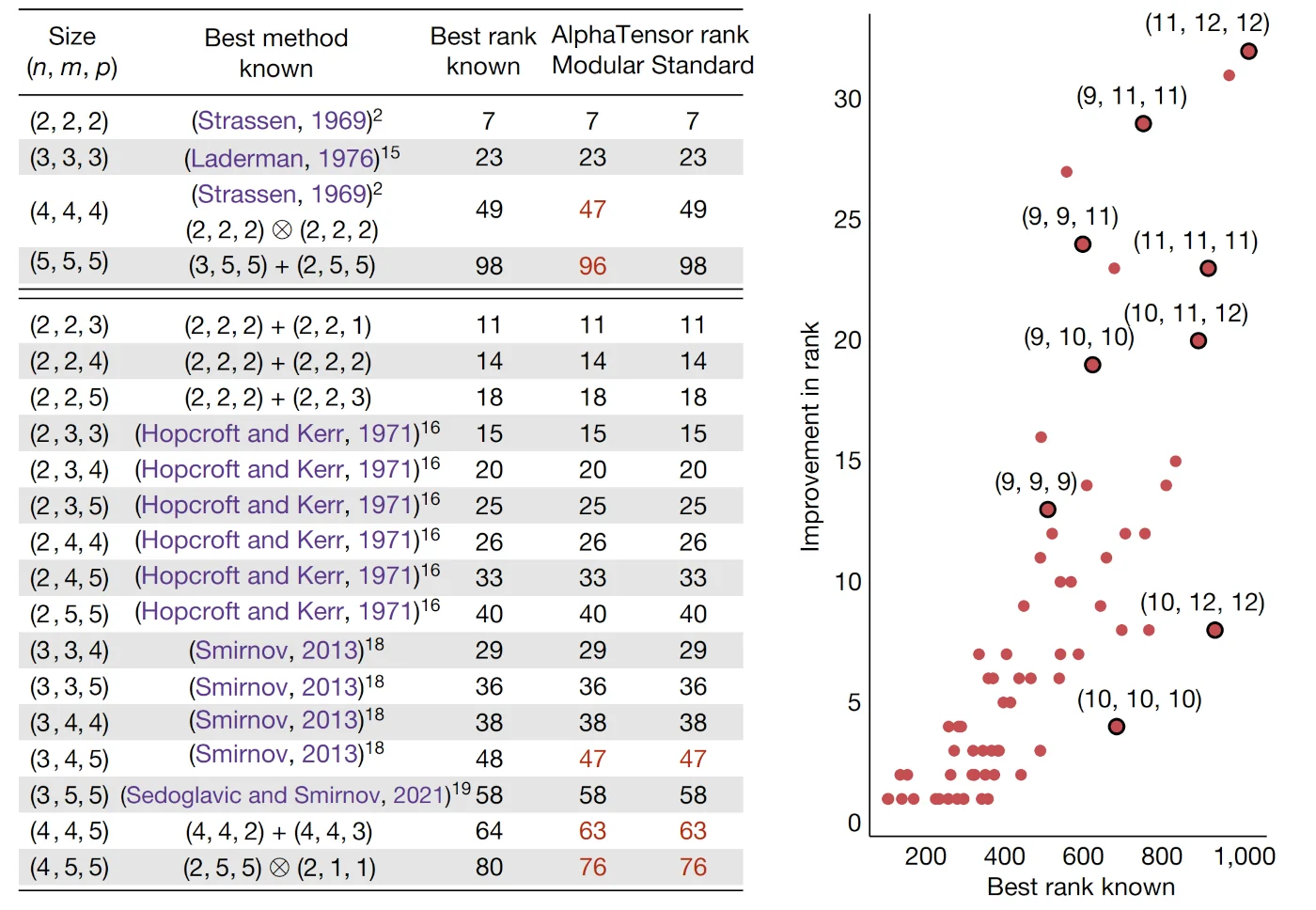
We train a single instance of AlphaTensor to find solutions for all combinations of matrix sizes less than 5, sampling a random set of sizes at the start of each game. AlphaTensor can re-discover many known optimal algorithms (e.g. Strassen), but also discovers algorithms that are faster than the currently best known approaches, highlighted in red:
In addition to strictly optimizing for the number of multiplications, AlphaTensor can also be used to directly optimize for the execution time of matrix multplications on real hardware:
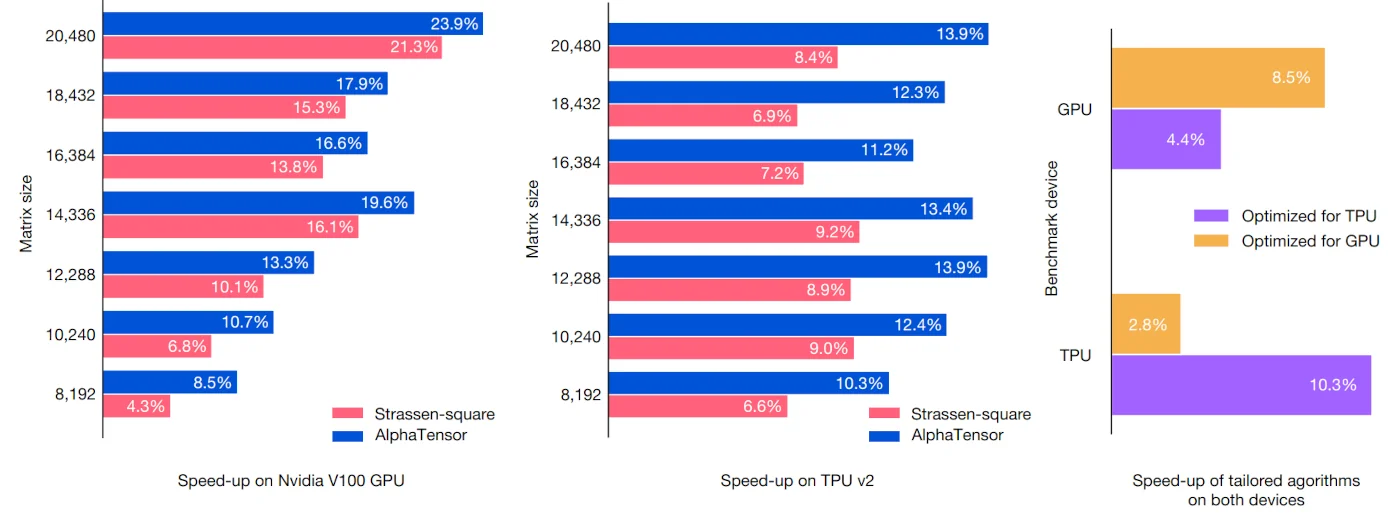
This is useful because an algorithm that is optimal for one device may perform poorly on another, and vice versa - see the right-most bar chart above.
Discussion
Starting from scratch, AlphaTensor discovers a wide variety of matrix multplication algorithms. Beyond advancing mathematical knowledege, these discoveries have direct practical impact, as matrix multplication is at the core of many computational tasks. In addition to matrix multplication, AlphaTensor can also be extended to other related problems, such as computations of rank or matrix factorization.
For more details, please see our [cached]official blog post and the [cached]Nature paper itself.